The full gradient of a property \(Q\) at a face can can be interpolated from the cell-based gradient. The surface-normal contribution is then represented by:

\[\snGrad Q = \vec{n} \dprod \left( \grad Q \right)_f\]

where \(\vec{n}\) is the face unit normal. The stencil for the gradient calculation at the face, \(f\), between cells P and N is described by the following figure: 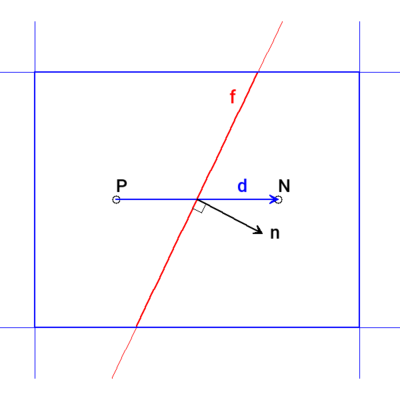where the vector \(\vec{d}\) joins the two cell centres. A variety of schemes are available that differ in their application based on the angle, \(\theta\), between the \(\vec{d}\) and \(\vec{n}\) vectors, representing the degree of non-orthogonality.

Usage🔗

Surface-normal gradient schemes are specified in the fvSchemesfile under the snGradSchemes sub-dictionary using the syntax:

snGradSchemes
{
    default         none;
    snGrad(Q)       <snGrad scheme>;
}

Options🔗

• Corrected surface-normal gradient scheme
• Face-corrected surface-normal gradient scheme
• Limited surface-normal gradient scheme
• Orthogonal surface-normal gradient scheme
• Uncorrected surface-normal gradient scheme

Example🔗

Further information🔗

Source code:

• $FOAM_SRC/finiteVolume/finiteVolume/snGradSchemes/snGradScheme

API:

• Foam::fv::snGradScheme