- Solver: scalarTransportFoam
- Repository link: $FOAM_TUTORIALS/verificationAndValidation/schemes/divergenceExample
Introduction🔗
This example case comprises a 2-D box section, across which a uniform flow is applied. A passive scalar is introduced across the left boundary, and transported across the domain. By looking at the profile of the scalar part way across the section, we can determine the characteristics of our divergence scheme selection.
Case set-up🔗
A frozen flow field is set by the U field, and the passive scalar by the
T field. The time step is set to 5e-3s, leading to a maximum Courant
number of 0.5. The impact of the choice of numerical scheme is assessed by
varying the div scheme entry of the fvSchemes file:
divSchemes
{
div(phi,T) Gauss <interpolation scheme>
}
Mesh🔗
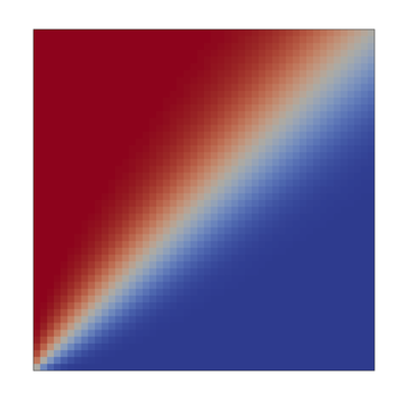
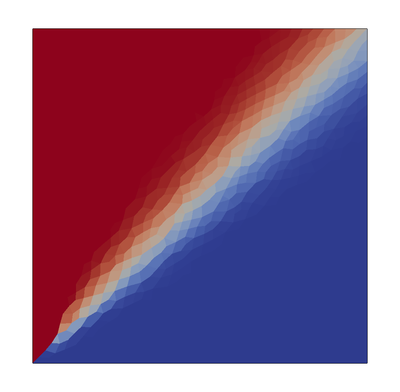
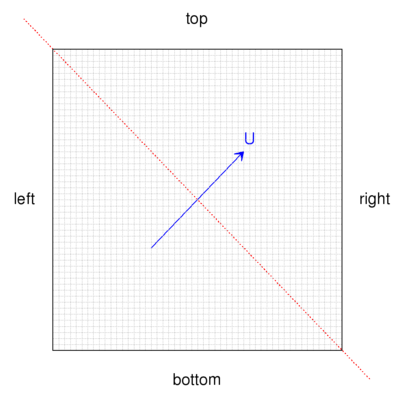
A 2-D square domain with side length 1m is employed, with two mesh variants: 50x50 uniform quad cells and a triangle mesh:
 |
 |
Results are sampled at the location shown by the dashed line.
Boundary conditions🔗
The velocity is set to a constant value of (1,1,0) m/s across the domain with the following boundary conditions:
| Patch | Type | Value |
|---|---|---|
| left | fixedValue | (1,1,0) |
| right | zeroGradient | |
| top | zeroGradient | |
| bottom | fixedValue | (1,1,0) |
| frontAndBack | empty |
The passive scalar is initialised to zero and evolved with the velocity
field by assigning a value of 1 at the left boundary:
| Patch | Type | Value |
|---|---|---|
| left | fixedValue | 1 |
| right | zeroGradient | |
| top | zeroGradient | |
| bottom | fixedValue | 0 |
| frontAndBack | empty |
Results🔗
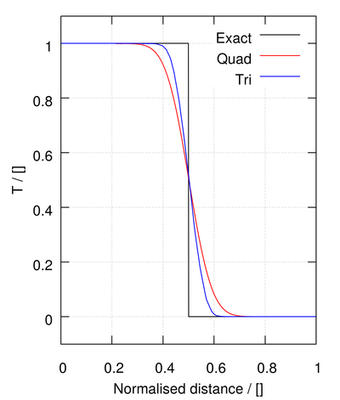
The following sequence of images show the steady results for the spatial distribution of the passive scalar. First order methods such as upwind show their diffusive characteristic, whereby the sharp profile is heavily smeared as the flow is not aligned with the mesh:
The linear scheme is a second order method, able to better preserve the step profile, but at the expense of unboundedness:
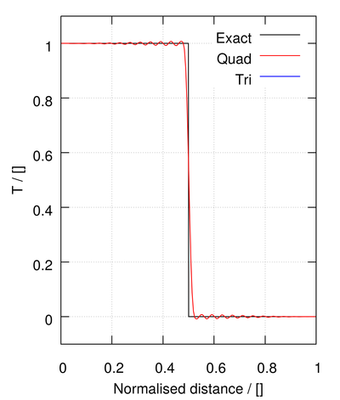
The remaining methods provide a blend between first order upwind and second order linear methods:
 |
 |
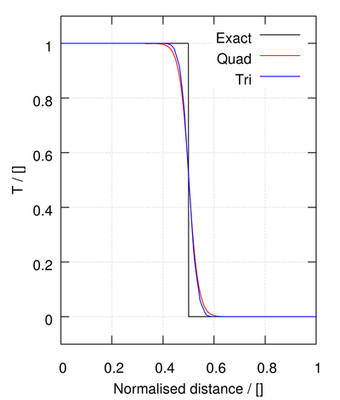 |
| Minmod | ||
 |
 |
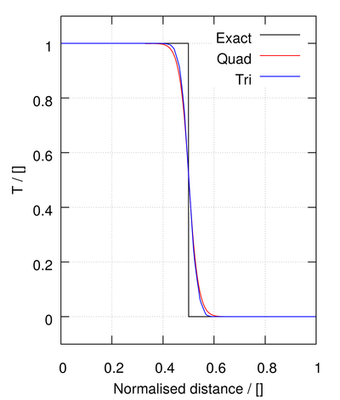 |
| SFCD | ||
 |
 |
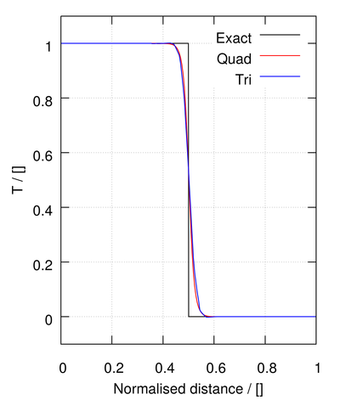 |
| limitedLinear 1.0 | ||
 |
 |
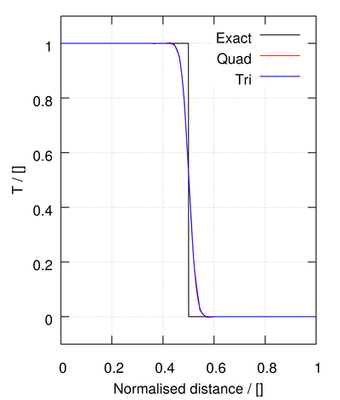 |
| vanLeer | ||
 |
 |
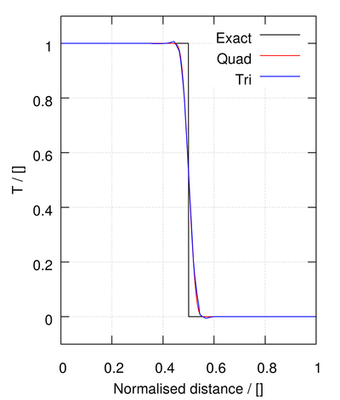 |
| MUSCL | ||
 |
 |
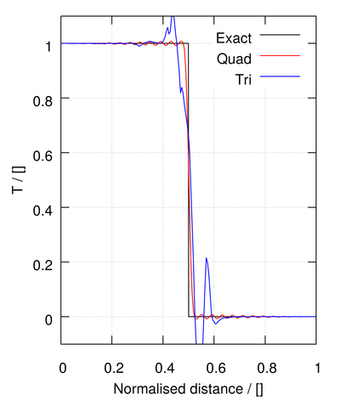 |
| midPoint - equivalent to linear on isotropic structured meshes | ||
 |
 |
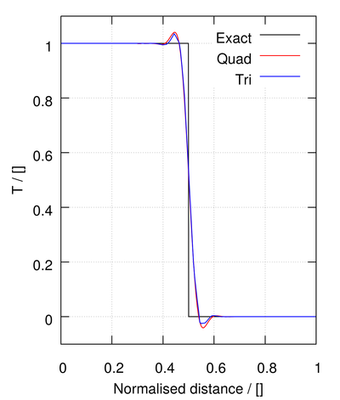 |
| linearUpwind | ||
 |
 |
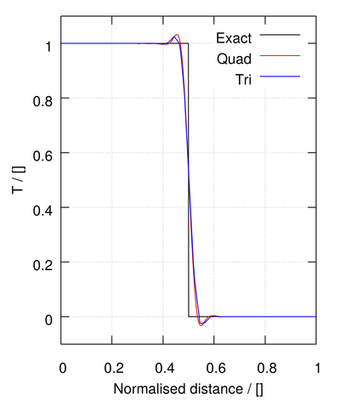 |
| QUICK |