Overview🔗
- Based on https://turbmodels.larc.nasa.gov/naca0012_val.html [53]
- References: Gregory-O’Reilly (1970) [21], McCroskey (1987) [47], Ladson (1988) [32], Spalart-Allmaras (1994) [69], and Krist et al. (1997) [29]
- See the resources section for additional data files
Flow physics:
- External flow
- Steady
- High Reynolds number
- Low Mach number, subsonic
- Newtonian, single-phase, incompressible, non-reacting
Solver:
Tutorial case:
Physics and Numerics🔗
Physical domain:
- The case is a two-dimensional airfoil located around the centre of a
computational domain whose dimensions are considerably larger than the
chord-length of the airfoil.
- \(x\): Longitudinal direction (mean flow direction)
- \(y\): Spanwise direction (statistically homogeneous direction)
- \(z\): Vertical direction (wall-normal direction)
- \(O\): Origin at the leading edge of the airfoil
Physical modelling:
- Reynolds number based on local chord length:
\(\text{Re}_c = U_x \, c \, \nu^{-1} \approx 6\times10^6\)
- Streamwise far-field flow speed: \(U_x = 51.4815\) [m⋅s-1]
- Characteristic length (Local chord length of the airfoil): \(c = 1.0\) [m]
- Kinematic viscosity of fluid: \(\nu_\text{fluid} = 8.58 \times 10^{-6}\) [m2⋅s-1]
- Mach number: \(\text{Ma} = U_x / U_s \approx 0.15\)
- Speed of sound: \(U_s = 343.21\) [m⋅s-1]
- Turbulence model: Spalart Allmaras
Numerical domain modelling:
- Shape: extruded C-grid
- Dimensions: \((x, y, z) \approx (985.5, 1.0, 1015.6)\) [m]
- Sketch (View direction to \(y\)-positive):
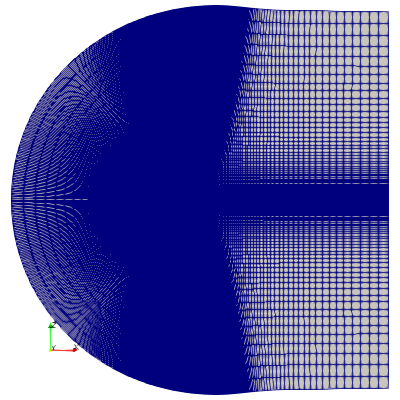
Spatial domain discretisation:
- Mesh type: hexahedral cells in plot3d format
- Mesh converter: plot3dToFoam
- Number of cells, \(N\) : \((N_x, N_y, N_z) = (257, 1, 897)\)
- First wall-normal cell centre height: \(\Delta_y^+ < 1\)
- Mesh detail (View direction to \(y\)-positive):
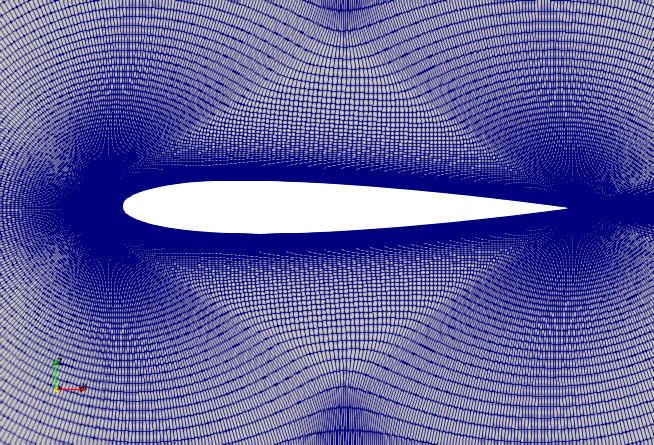
Equation discretisation:
Spatial derivatives and variables:
- Gradient: Gauss linear
- Divergence:
-
default: Gausslinear -
div(phi,U):bounded GausslinearUpwindgrad(U) -
div(phi,nuTilda):bounded Gauss linearUpwind grad(nuTilda)
-
- Laplacian:
Gaussian linear corrected - Surface-normal gradient: corrected
Temporal derivatives and variables:
-
ddtSchemes: steadyState
Numerical boundary conditions:
- Velocity, \(\mathbf{U}\)
| Patch | Condition | Value [m⋅s-1] |
|---|---|---|
| Inlet | freestreamVelocity | \(\mathbf{U}_\alpha\) |
| Outlet | freestreamVelocity | \(\mathbf{U}_\alpha\) |
| Sides \(\text{(}y\)-dir) | empty | - |
| Aerofoil | fixedValue | (0.0, 0.0, 0.0) |
| α | U α |
|---|---|
| \(\alpha = 0^o\) | (51.4815, 0.00, 0.0000) |
| \(\alpha = 10^o\) | (50.6994, 0.00, 8.9397) |
| \(\alpha = 15^o\) | (49.7273, 0.00, 13.3244) |
- Kinematic pressure,
p
| Patch | Condition | Value [m2⋅s-2] |
|---|---|---|
| Inlet | freestreamPressure | 0.0 |
| Outlet | freestreamPressure | 0.0 |
| Sides \(\text{(}y\)-dir) | empty | - |
| Aerofoil | zeroGradient | - |
- Turbulent kinematic viscosity,
nut(i.e. \(\nu_t\))
| Patch | Condition | Value [m2⋅s-1] |
|---|---|---|
| Inlet | freestream | \(8.58e^{-6} \approx \nu_\text{fluid}\) [54] |
| Outlet | freestream | \(8.58e^{-6}\approx \nu_\text{fluid}\) [54] |
| Sides \(\text{(}y\)-dir) | empty | - |
| Aerofoil | fixedValue | 0.0 [54] |
- Spalart-Allmaras model modified viscosity,
nuTilda(i.e. \(\tilde{\nu}\))
| Patch | Condition | Value [m2⋅s-1] |
|---|---|---|
| Inlet | freestream | \(3.432e^{-5} \approx 4 \nu_\text{fluid}\) [54] |
| Outlet | freestream | \(3.432e^{-5}\approx 4 \nu_\text{fluid}\) [54] |
| Sides \(\text{(}y\)-dir) | empty | - |
| Aerofoil | fixedValue | 0.0 [54] |
Solution algorithms and solvers:
- Pressure-velocity: SIMPLE
- Parallel decomposition of spatial domain and fields: Not applicable
- Linear solvers:
| Field | Linear Solver | Smoother | Tolerance (rel) |
|---|---|---|---|
U |
smooth | GaussSeidel | 0.01 |
p |
GAMG | GaussSeidel | 0.01 |
nuTilda |
smooth | GaussSeidel | 0.01 |
Results🔗
List of metrics:
- Lift coefficient \(\mathrm{C}_\mathrm{L}\) vs. Angle of attack \(\alpha\)
- Drag coefficient \(\mathrm{C}_\mathrm{D}\) vs. Angle of attack \(\alpha\)
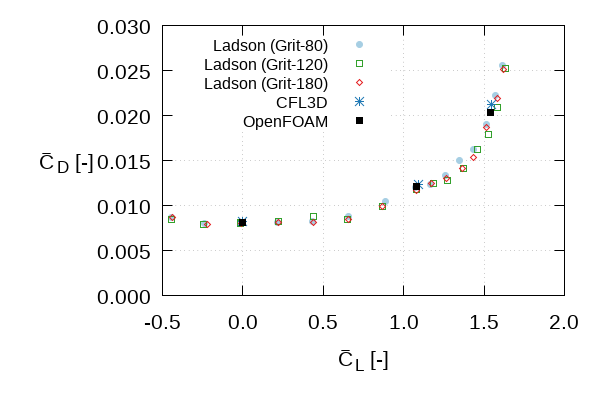
- Drag coefficient \(\mathrm{C}_\mathrm{D}\) vs. Lift coefficient \(\mathrm{C}_\mathrm{L}\)
- Surface pressure coefficient \(\mathrm{C}_p\) vs. Normalised chord length \(x/c\)
- Surface skin friction coefficient \(\mathrm{C}_f\) vs. Normalised chord length \(x/c\)
- \(\{\overline{\cdot}\}\) is the time-averaging operator
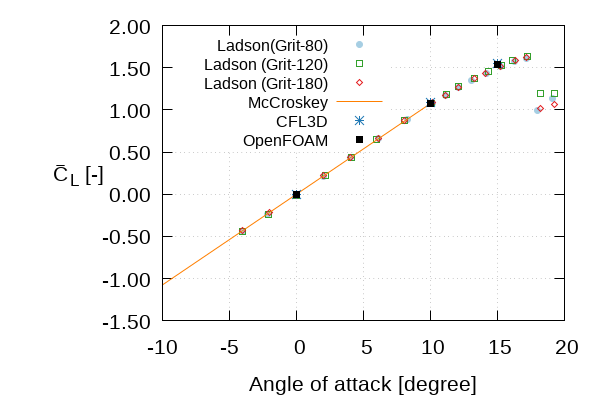 |
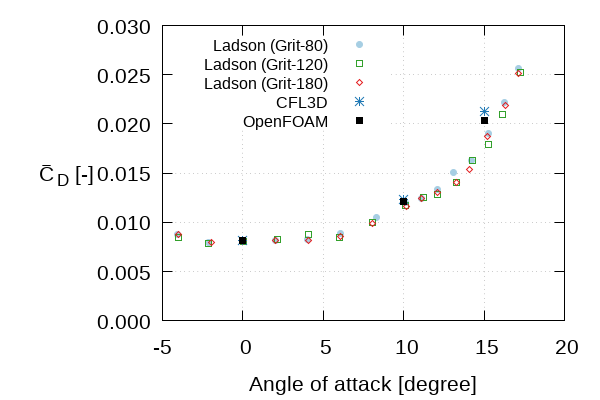 |
 |
![Surface pressure coefficient vs. Normalised chord length at α=0 [degree]](CP-xc-Alpha-0.png) |
![Surface pressure coefficient vs. Normalised chord length at α=10 [degree]](CP-xc-Alpha-10.png) |
![Surface pressure coefficient vs. Normalised chord length at α=15 [degree]](CP-xc-Alpha-15.png) |
![Surface skin friction coefficient vs. Normalised chord length at α=0 [degree]](CF-xc-Alpha-0.png) |
![Surface skin friction coefficient vs. Normalised chord length at α=10 [degree]](CF-xc-Alpha-10.png) |
![Surface skin friction coefficient vs. Normalised chord length at α=15 [degree]](CF-xc-Alpha-15.png) |
Resources🔗
Note: Links will take you to the NASA website
Mesh🔗
Datasets for verifications (plain text)🔗
Lift and drag coefficients vs angle of attack
Pressure distribution vs local chord length
Lift coefficient vs angle of attack
Skin friction coefficient vs local chord length
